Unit 9 transformations homework 3 rotations answer key – Delve into the intricacies of rotations in the coordinate plane with Unit 9 Transformations Homework 3: Rotations Answer Key. This comprehensive guide provides a thorough understanding of rotation concepts, problem-solving techniques, and practical applications.
Master the art of performing rotations using matrices, analyze problems related to rotations, and identify common errors to enhance your problem-solving skills. Explore the diverse applications of rotations in engineering, physics, and computer graphics, gaining valuable insights into their significance in various fields.
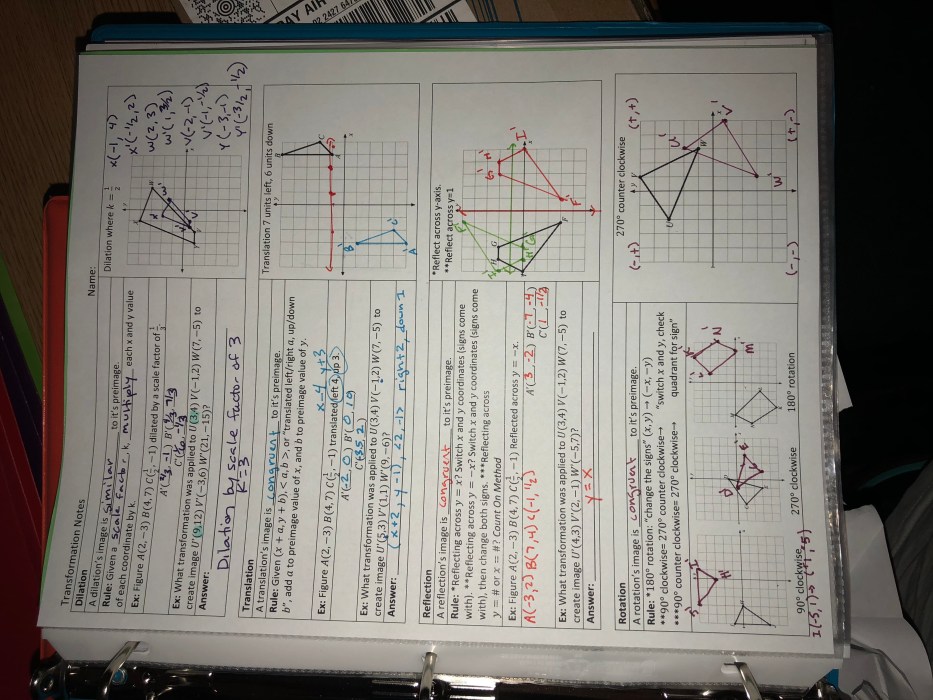
Transformations: Rotations: Unit 9 Transformations Homework 3 Rotations Answer Key
Transformations are mathematical operations that manipulate geometric shapes. Rotations are a type of transformation that involves turning a shape around a fixed point called the center of rotation.
Rotations in the Coordinate Plane, Unit 9 transformations homework 3 rotations answer key
In the coordinate plane, rotations are described by the angle of rotation and the direction of rotation. The angle of rotation is measured in degrees or radians, and the direction of rotation is specified as clockwise or counterclockwise.
To perform a rotation, we use a rotation matrix. A rotation matrix is a 2×2 matrix that represents the rotation transformation. The rotation matrix for a rotation of θ degrees counterclockwise about the origin is given by:
$$\beginbmatrix \cos \theta &
\sin \theta \\\ \sin \theta & \cos \theta \endbmatrix$$
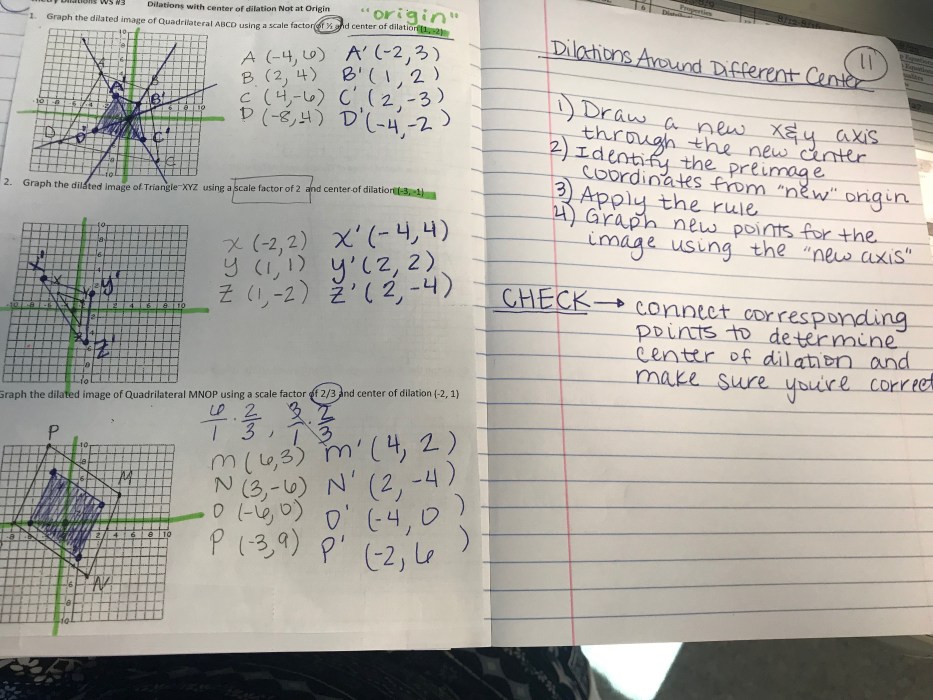
Transformations Homework 3: Rotations
Homework 3 contains several problems related to rotations. These problems involve rotating shapes around different centers of rotation and using rotation matrices to perform rotations.
To solve these problems, we need to understand the concepts of rotations and how to apply rotation matrices. We also need to be able to identify the center of rotation and the angle of rotation for each problem.
Answer Key for Rotations
The answer key for Homework 3 provides the correct answers to the rotation problems. The answers are explained step-by-step, and alternative approaches are discussed.
The answer key is a valuable resource for students who want to check their work and learn from their mistakes.
Applications of Rotations
Rotations have numerous practical applications in various fields, including engineering, physics, and computer graphics.
- In engineering, rotations are used to design and analyze mechanical systems, such as gears and turbines.
- In physics, rotations are used to describe the motion of objects, such as planets and electrons.
- In computer graphics, rotations are used to create 3D models and animations.
Common Queries
What is the concept of rotation in the coordinate plane?
Rotation in the coordinate plane involves rotating a figure around a fixed point by a specified angle, resulting in a new position and orientation.
How do I perform rotations using matrices?
Matrices provide a systematic method for performing rotations. By applying the appropriate rotation matrix to the coordinates of a figure, you can determine its new position after rotation.
What are common errors to avoid when solving rotation problems?
Common errors include incorrectly identifying the center of rotation, applying the incorrect rotation angle, or failing to consider the direction of rotation.